统计学的威力——利用本福特定律检查数据造假
By 小二
at 2020-02-03
在实际生活得出的数据中,不同数字开头的数字出现机率是有规律可循的。如果不遵从这个规律,那么就表明数据存在人为伪造。
1935 年,美国的一位叫做本福特的物理学家在图书馆翻阅对数表时发现,对数表的头几页比后面的页更脏一些,这说明头几页在平时被更多的人翻阅。
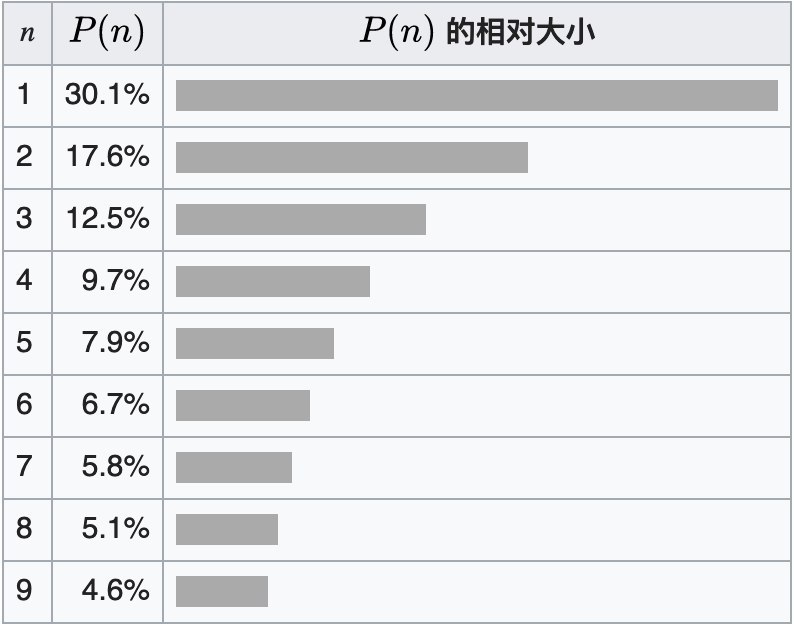
本福特再进一步研究后发现,只要数据的样本足够多,数据中以 1 为开头的数字出现的频率并不是 1/9,而是 30.1%。而以 2 为首的数字出现的频率是 17.6%,往后出现频率依次减少,9 的出现频率最低,只有 4.6%。
数学原理:
在 $b$ 进位制中,以数 $n$ 起头的数出现的机率为:
参考资料:
小二在线教授统计学!
electron8964
at 2020-02-03
1
@electron8964 #1 支持 $\LaTeX$ 真的是正确的选择。
小二
at 2020-02-03
2
別迷信這種,真實數據除以10,就破解了
拿衣服
at 2020-02-03
3
除以10,再用前幾天的數據,這種造假都符合本福特定律
拿衣服
at 2020-02-03
4
除以任意常數應該都不會改變符合本福特定律的特性
拿衣服
at 2020-02-03
5
